Ломаная линия

Метод polyline вычерчивает ломаную линию. В качестве параметра метод получает массив типа TPoint. Каждый элемент массива представляет собой запись, поля х и у которой содержат координаты точки перегиба ломаной. Метод Polyline вычерчивает ломаную линию, последовательно соединяя прямыми точки, координаты которых находятся в массиве: первую со второй, вторую с третьей, третью с четвертой и т. д.

В качестве примера использования метода Polyline в листинге 10.3 приведена процедура, которая выводит график изменения некоторой величины. Предполагается, что исходные данные находятся в доступном процедуре массиве Data (тип Integer).

Листинг 10.3. График функции (использование метода Polyline)

procedure TForml.Button1Click(Sender: TObject);

var

gr: array[1..50] of TPoint; // график — ломаная линия

x0,y0: integer; // координаты точки начала координат

dx,dy: integer; // шаг координатной сетки по осям X и Y

i: integer; begin

х0 := 10; у0 := 200; dx :=5; dy := 5;

// заполним массив gr

for i:=l to 50 do begin

gr[i].x := x0 + (i-l)*dx;

gr[i].y := y0 - Data[i]*dy;

end;

// строим график

with forml.Canvas do begin

MoveTo(x0,y0); LineTo(x0,10); // ось Y

MoveTo(x0,y0); LineTo(200,y0); // ось X

Polyline(gr); // график

end;

end;

Метод Polyline можно использовать для вычерчивания замкнутых контуров. Для этого надо, чтобы первый и последний элементы массива содержали координаты одной и той же точки. В качестве примера использования метода Polybine для вычерчивания замкнутого контура в листинге 10.4 приведена программа, которая на поверхности диалогового окна, в точке нажатия кнопки мыши, вычерчивает контур пятиконечной звезды (рис. 10.5). Цвет, которым вычерчивается звезда, зависит от того, какая из кнопок мыши была нажата. Процедура обработки нажатия кнопки мыши (событие MouseDown) вызывает процедуру рисования звезды starLine и передает ей в качестве параметра координаты точки, в которой была нажата кнопка. Звезду вычерчивает процедура starLine, которая в качестве параметров получает координаты центра звезды и холст, на котором звезда должна быть выведена. Сначала вычисляются координаты концов и впадин звезды, которые записываются в массив р. Затем этот массив передается в качестве параметра методу Polyline. При вычислении координат лучей и впадин звезды используются функции sin и cos. Так как аргумент этих функций должен быть выражен в радианах, то значение угла в градусах домножается на величину pi/18о, где pi — это стандартная именованная константа равная числу л.

Листинг 10.4. Вычерчивание замкнутого контура (звезды) в точке нажатия кнопки мыши

unit Stars_; interface

uses

Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls;

type

TForm1 = class(TForm)

procedure FormMouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Forml: TForml;

implementation

f$R *.dfm}

// вычерчивает звезду

procedure StarLine(x0,y0,r: integer; Canvas: TCanvas);

// x0,y0 — координаты центра звезды

//r — радиус заезды var

р : array [1.. 11] of TPoint;

// массив координат лучей и впадин

a: integer; // угол между осью ОХ и прямой, соединяющей

// центр звезды и конец луча или впадину i: integer;

begin

а := 18; // строим от правого гор. луча

for i:=l to 10 do begin

if (i mod 2=0) then begin // впадина

p[i].x := x0+Round(r/2*cos(a*pi/180) ) ;

p[i] .y:=y0-Round(r/2*sin(a*pi/180) ) ;

end

else

begin // луч

[i] .x:=x0+Round(r*cos (a*pi/180) ) ;

[i] .y:=y0-Round(r*sin(a*pi/180) ) ;

end;

a := a+36;

end;

p[ll].X := p[l].X; // чтобы замкнуть контур звезды

Canvas. Polyline (р) ; // начертить звезду

end;

// нажатие кнопки мыши

procedure TForm1 . FormMouseDown { Sender : TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

if Button = mbLeft // нажата левая кнопка?

then Form1. Canvas . Pen . Color : = clRed

else Form1. Canvas. Pen. Color := clGreen;

StarLine(x, y, 30, Forml. Canvas );

end;

end.

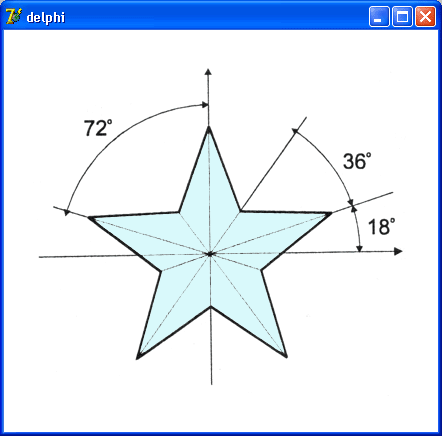
Рис.10.5. Звезда

Примечание

Обратите внимание, что размер массива р на единицу больше, чем количество концов и впадин звезды, и что значения первого и последнего элементов массива совпадают.